Encryption by Encryption by Public Discussion in 1974
這種加密方法是類似於D-H公開交換金鑰方法的精神,但也因為這樣所以man-in-the-middle attack也對此加密方法有效。
一樣用Alice跟Bob做例子,假設Alice要運用此演算法加密,它先將明文算到x次方後mod p,$C_1 \ \ = \ \ m^x \ \ mod \ \ p$,將$C_1$傳給Bob。接著Bob收到$C_1$後,將它算到y次方mod p,$C_2 \ \ = \ \ C_1^y \ \ mod \ \ p \ \ = \ \ m^{xy} \ \ mod \ \ p$,然後將$C_2$傳回給Alice。(注意這傳送過程中x跟y都只有加密的那個人才知道)
接著Alice用乘法反元素算出x’,將Alice一開始加密的x消掉,記算出$C_3 \ \ = \ \ C_2^{x'} \ \ mod \ \ p \ \ = \ \ m^y \ \ mod \ \ p$,接著將$C_3$傳給Bob。最後Bob依樣畫葫蘆再計算出y’消掉y,計算出$m \ \ = \ \ C_3^{y'} \ \ mod \ \ p$就得到m啦!
$(x' \ \ \times \ \ x \ \ \equiv \ \ 1 \ \ (mod \ \ p-1), \ \ y' \ \ \times \ \ y \ \ \equiv \ \ 1 \ \ (mod \ \ p-1) )$
Security Consideration of RSA
接下來探討RSA的安全性,RSA演算法第一步就是要找質數,我們來看一下”質數”這東西:首先先介紹Prime-counting function π(x), π(x)代表的是x以下總共有多少個質數,而當x趨近於無窮大時,$\lim_{x \rightarrow \infty} \frac{\pi (x)}{x/ln(x)} \ \ = \ \ 1$ ,而我們在實作時所選的質數大概是512 bit,那麼所涵蓋的質數可以看到下表:
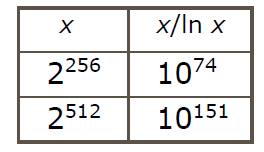
所以不太需要擔心所選的質數會跟別人一樣。而質數的密度有多高呢?注意一下π(x) = x/ln(x),我們可以看成1/ln(x)就是質數的密度,這是在小於x底下的所有正整數有1/ln(x)是質數,而所有小於x的正整數有一半是奇數,我們知道質數一定是奇數,所以如果直接從奇數裡面來抓質數的話密度又更高了,在奇數裡質數所佔的密度為2/ln(x),我們x代512的話可以得到2/ln(512) = 1/177,每177個奇數數裡面就有一個質數。
接下來分析攻擊RSA的方法,要攻擊的話會想要做的事情是取得private key(d, n),而public key(e, n)是已知的。所以如果我們要知道d的話必須知道φ(n)才能計算,而不管攻擊者是直接計算出d或者是直接計算出φ(n),這兩者都相當於質因數分解n。而Shamir & Tromer有發展出TWIRL device可以分解RSA 1024bit,不過需要耗費1000萬美金,6個禮拜才有辦法破解,成本相當高。
而大質數得質因數分解目前還是個難題,但如果這個大質數是由一群小質數所組成,又或者因數裡只有一個較大的質數,則能夠用quadratic sieve分解開來,所以之後發展出了strong prime的結構:
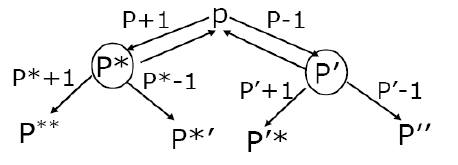
這結構是這樣的:一個大質數P在+1或-1後一定能被2分解,分解完後如果還有其他小質數沒關係,但一定要有一個很大的質數在,而這個很大的質數暫且稱做P’,而P’再經過+1或-1後,仍然還要有剛剛講的特性,必須分解完後還要再擁有一個較大的質數,此結構稱為strong prime。雖然現在的generalized number field (GNF) sieve分解方法不管你是不是strong prime都沒差,不過有些特殊系統還是會需要用到此特性。
而在選擇質數pq時,最好不要選擇太接近的值,不然很容易被暴力破解開來。考慮下列式子:
則我們能利用$ \sqrt{n}$來猜pq。舉個例子:假設p=13, q=11,則$ \sqrt{n} \ \ \approx \ \ 12 $,我們先猜$ \frac{p \ \ + \ \ q}{2} \ \ = \ \ 12$,代回剛剛式子很快就能得出p=13, q=11,如果代出來不對則繼續猜13,14…..,p跟q很接近時很快就會被代出來。而有些情況為了讓解密時加速會選較小的d,有一種針對d小於$ \frac{1}{3} N^{ \frac{1}{4}}$情況的攻擊,Wieners attack,在幾分鐘內就能解出pq。
random padding
此方法可以避免掉很多實作時出現的問題,概念是這樣的:原本訊息為m,經過random padding後,會在m的前面或後面加上n bit的隨機值變為m’,在將此m’進行加密。而實作時遇到的問題分為下列幾項:
Guessable message attack:此攻擊運用在當你傳送的message是固定的集合時,觀察者可以將那些故定的集合通通拿去加密,接著只要觀察通訊時傳送的通道,比對其密文就能得知鄉對應的明文。但如果使用了random padding則一樣的訊息加密後是不一樣的密文,此攻擊便無效。
有時為了加密方便會設比較小的e,此時可能會發生$m^e$比n還小,造成mod沒有效果,這時解密就變成了簡單的問題了。這個問題一樣可以經由padding解決,在message之前padding到超過n的bit數,使得就算e不夠大也會讓$m^e$大於n。
而另一種情況是當你傳了同樣的訊息給了三個不同的人時,由於這三個人所使用的n都不一樣,造就了這三個密文的計算方式形同CRT,利用這一點能夠mapping回message。下圖為e=3時的例子:

如上圖所示,$m^3$就是CRT裡面的大世界,$C_1$, $C_2, $C_3$分別是$n_1$, $n_2$, $n_3$的小世界,所以利用$C_1$, $C_2, $C_3$變能計算CRT mapping回大世界的$m^3$。這問題解決方法一樣是padding,random padding完後所有的m都不一樣了,故CRT失效。
那如果使用一樣的n會造成什麼問題呢?考慮以下情境:今天有一家公司每天都必須頻繁的傳遞機密訊息,但每次傳訊息之前都必須先查詢接收方的public key,這一點實在是非常麻煩,因為每個人的n都不一樣,e就更不用說了,於是這家公司想到了一個妙招,他們直接固定n,而且e直接設為接收方的email帳號,如此一來要記機密訊息之前就不需要查詢對方的key了。上述方法看似沒問題,每個人的key都不一樣,問題就在n是相同的,如果是公司成員會有private key d,當然不能讓公司成員知道d,必須要設計成只能使用不能知道其內容,不然知道d就能分解pq了。而Common-modulus attack可以利用同一訊息傳給兩個不同人(同一個n)情況下產生作用。假設我今天用$e_a$加密m傳$C_a$給Alice,用$e_b$加密m傳$C_b$給Bob,那麼攻擊者知道$C_a$, $C_b$後,他可以先用歐基理得輾轉相除計算$re_a \ \ + se_b \ \ = \ \ 1 $,得到r跟s後,變能計算出m:
接著是簽章的部分,由於簽章的key就是解密的key,因此不要隨便幫別人亂簽章,很有可能是有心人士要你幫他做解密。假設今天有人要你幫他簽章,他會傳$r^e \ \ \times \ \ C$給你,C是他無法解密的,r是他自己產生的,因此當你簽完張後其實是看不出他是有意義的訊息,因為被r破壞掉了,而你幫他做完解密他自己再乘上r的反元素變能得到C的原文。
而簽章其實就是對訊息冠上一個d次方的動作,所以即使你本人沒有簽章也會有一堆的數字可以是用你的d做次方運算之後的結果。因此我們在簽章時都會伴隨著hash function,除了e驗證完是否為簽章外,你還要告訴我這個hash值是對應到哪個message。
multiplicative attack:受害方今天用了RSA簽過了$m_1$跟$m_2$,那麼攻擊者可以製造出任何的$(m_1)^j (m_2)^k$形式的簽章。
Rabin’s Signature Schemes
由於rabin在做解密時會產生四個根,而加密方一定要告訴解密方傳送的訊息是哪一個,因此有了接下來的方法,雖然此方法很漂亮,但是卻不可行。此方法只需要兩個bit就能告訴接收方說我今天傳的是哪個訊息,第一個bit是Jacobian symbol,第二個bit是告訴接收方我的message是屬於正根還是負根。既然此方法能利用兩個位元從四個選項中挑出正確的訊息,那麼第一個位元應該就能夠在這四個當中砍半挑出兩個,而第二個位元在從這兩個當中選出正確的訊息。那Jacobian symbol是如何從四個選項中刪除兩個錯的呢?
當模數p擁有4n+3此種特性時,在此模數底下數係的加法反元素的Jacobian symbol,會恰好是此數的Jacobian symbol的加法反元素(也就是Jacobian symbol此函式為奇函式)。舉個例子:J(x) = -J(-x)。這代表著如果今天x為$QR_p$時,-x一定為$NQR_p$。我們只要實際代個數字進去便能得知:
$J(-x) \ \ = \ \ (-x)^{(p-1)/2} \ \ = \ \ (-x)^{(4n+3-1)/2} \ \ = \ \ (-x)^{2n+1} \ \ = \ \ -J(x)$但這種方法是行不通的….加密方是沒辦法算Jacobian symbol的….GG
所以之後的方法就比較沒有這麼”文明”,就直接在訊息裡面塞一堆1或一堆0來辨認。當然之前所講的padding小技巧都能拿來這邊用,但特別注意別全部都用radom值,因為你就是要用這個特徵來辨認啊啊啊。而rabin這個加密法非常厲害,他能夠被證明說如果能夠破解rabin演算法,就相當於破解了大質數的因數分解。那是怎麼做到的呢?其實就是之前所講的解密方會解出四個訊息,如果沒有固定給使用者訊息的話,使用者可以將納四個訊息做加減再跟n取最大公因數,有一半的機會能分解pq。因此今天如果我使用了rabin加密,而有位天才發明了解密方法,不管他是如何辦到他就事有辦法解出message,那我今天就自己先將m加密,再送到那位天才的解密器解密,用剛剛的方法多丟幾次就能分解pq了。
而一樣的概念拿來做攻擊,一樣是用簽章的key就是解密的key這點,我自己加密m完後丟給受害者簽章,簽完後他如果隨機挑四個答案的其中一個給我,那我就可以利用上述攻擊分解pq。所以最安全的做法就是剛剛所講到的padding一些特殊規則的符號來辨認正確的message,如果解完發現沒有此”特殊規則”則drop掉。