來源:chapter 2(51~54),chapter 3(1~23)
CBC Mode attack
concatenation attack
假設今天CBC不用來加密,它只用來進行MAC檢查碼計算,如果沒有處理好的話可能會遭受concatenation attack。它攻擊的樣貌是這樣的:假設今天有兩個合法字串P跟Q,P跟Q的檢查碼假如攻擊者都能接收的到,那麼攻擊者就能發送”類似”P+Q的字串給受害者,並且受害者接收到P+Q字串後經過MAC比對還是正確的。下面舉個實際例子:
假設P: $(P_1, \ \ P_2, \ \ ,..., \ \ P_n)$,Q: $(Q_1, \ \ Q_2, \ \ ,..., \ \ Q_t)$,P的檢查碼為$MAC_1$,Q的檢查碼為$MAC_2$,如下圖所示:
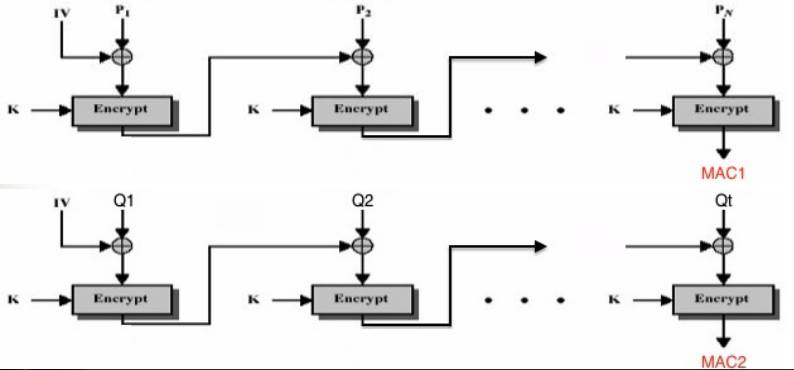
假如今天傳送方將P跟Q用明文傳送給接收方,並且後面附帶檢查碼,那麼攻擊者能夠將P跟Q串在一起,並且讓這串P+Q的檢查碼為$MAC_2$。如果要將這兩個字串串在一起應該會長的像下圖:

但這樣子串的話最後檢查碼一定不是$MAC_2$,沒關係,既然他是明碼,我們可以在$Q_1$上動手腳,假設他現在叫做x:
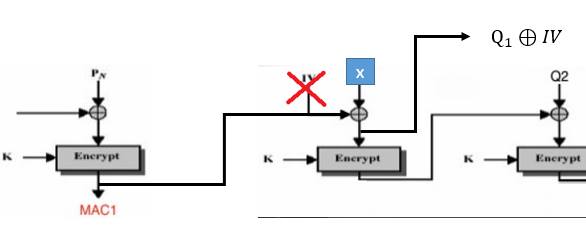
如果要讓最後的檢查碼為$MAC_2$的話,那麼就要讓$x \bigoplus MAC_1 \ \ = \ \ Q_1 \bigoplus IV$ ,因此 $x \ \ = \ \ Q_1 \bigoplus IV \bigoplus MAC_1$,如此一來攻擊者就能自行串接合法字串了。
假設傳送方知道了此種攻擊方法,那他就可能想說:阿我就把MAC在加密一次就好了啊~這樣攻擊者要XOR MAC時就崩潰了,沒錯,但是如果傳送方是直接用剛剛CBC計算的那把key加密,這樣攻擊者還是能夠自行連接字串的。假設今天攻擊者接收到的是加密過後的檢查碼,以及明文的字串P跟Q,如果要按照剛剛的攻擊的話必須要知道$MAC_1$的明文才有辦法,但是其實也可以這樣子做,由於0 XOR任何數會等於任何數,所以我在P跟Q中間多加了0,這樣會發生什麼事呢?
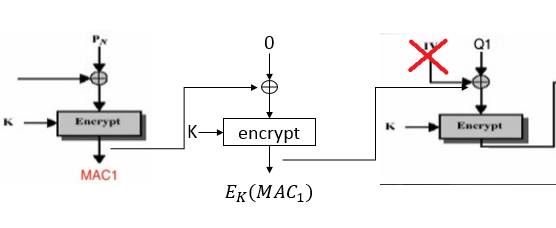
沒錯,這樣字串串在一起CBC計算時就會變成了把加密後的$MAC_1$拿去跟$Q_1$做XOR了,而加密後的$MAC_1$攻擊者也有,這麼一來問題就又回到了跟剛剛一樣的要如何把這整串檢查碼變為$MAC_2$了。所以攻擊者的連接字串只要變成$(P \ \ || \ \ 0 \ \ || \ \ (Q_1 \ \ ⊕ \ \ IV \ \ ⊕ \ \ E_K(MAC_1)), \ \ Q2,…, \ \ Qt)$,則最後的檢查碼就會是$MAC_2$。
所以比較安全的做法是將檢查碼用另外一把key來加密在傳送出去。
Attack-2: when CBC used as both encryption & MAC with a same key “K”
這邊要談的是當傳送密文時,你最後的檢查碼如果是直接將密文的最後一個cipher傳送出去,代表著你檢查碼跟加密用的是同一把key,這樣檢查碼基本上是無效的。因為攻擊者只要不改你的檢查碼改其他的cipher,你根本無從得知此訊息是否被竄改過(這是因為你收到的是密文,所以你並不知道正確的明文長什麼樣子,如果你將密文解密在加密一次,得到的會是一模一樣的密文)。因此你需要兩把key,一把拿來加密用一把拿來計算最後的檢查碼用。這樣子資料被竄改的話檢查碼會不一樣,因為檢查碼是從正確的明文計算得到的。
那如果拿第二把鑰匙只加密最後的檢查碼呢?其實仔細想想你最後的檢查碼如果是用原本加密那把key算出來的,你的用意應該是要辨別的出是否訊息被竄改過,而不是在MAC會不會被知道,所以一樣攻擊者不要改掉你的檢查碼就好了。
Number Theory
Infinitely Many Primes
這邊要證明的是質數有無限多個…..
這邊利用反證法:假設質數有限個,總共有n個質數,$\{ p_1, \ \ p_2, \ \ p_3, \ \ ... \ \ , \ \ p_n \}$,全宇宙就只有這些質數,那我今天做一件事情,把這些質數全部相乘再加一,$P \ \ = \ \ p_1 \ \ \times \ \ p_2 \ \ \times \ \ p_3 \ \ \times \ \ ... \ \ \times \ \ p_n \ \ + \ \ 1$,照剛剛的定義P這個數一定不是質數,那P一定可以被質因數分解,但是問題來了,看一下P是怎麼算出來的,發現P是所有質數的乘積加一,也就是說不管除哪個質數都會餘一無法整除,所以P是剛剛那群質數以外的質數,那這樣就造成矛盾了,因此質數為無限多個。
中間的一些基本定義我就直接跳過了…
Computing Inverse
假設我給你一個區間[1, n-1],在這區間內有一個值叫做a,a在這區間內的反元素為x,則我們定義ax mod n = 1。(由於加解密時我們不希望出現浮點數,因此我們用同餘的概念來解決反元素會出現浮點數的問題)。
證明:If gcd(a, n) = 1, then (ai mod n)≠(aj mod n) for each i, j such that 0 ≤ j < i < n.
這裡也是利用反證法:假設(ai mod n)=(aj mod n),則(ai - aj) mod n = 0,故 n | a(i-j),又gcd(a,n) = 1,所以 n | (i-j),而題目一開始講0 ≤ j < i < n,矛盾,得證(ai mod n)≠(aj mod n)。
在上述證明可以得出一個結果:任一x在小於n的情況下,ax mod n都不會重覆,而x範圍是0 ~ n-1,ax mod n的範圍也是0 ~ n-1,那麼假設今天輸入的值是依序從0到n-1,那麼輸出的值就會是這n個值的重新排列。既然是重新排列那麼ax mod n = 1一定存在且唯一。
證明:If gcd(a, n) = t > 1, then there does not exist x, 0 < x < n, such that ax mod n = 1
反證法:gcd(a, n) = t,所以 a = ta’, n = tn’,而ax mod n = 1,得到ax-1 = kn;ax - kn = 1, t(a’x-n’k) = 1,由於(a’x-n’k)為整數,所以t < 1,而題目一開始說t > 1,矛盾。
Reduced set of residues and Euler totient function
Reduced set of residues(RSR) mod n:意思是在小於n的正整數中所有與n互質的整數集合。
ex: For n=10, the RSR mod 10 is {1,3,7,9}
For n=7, the RSR mod 7 is {1 2 3 4 5 6}
Euler totient function:φ(n) φ(n)的意思是n的RSR個數。如果n為質數,則φ(n) = n - 1。
證明(1):For n = pq, p and q are primes, φ(n) = φ(p)φ(q) = (p-1)(q-1)
給定一集合s,此集合包含mod n之所有元素,s = {0, 1, 2, 3, … , pq-1},現在要算出RSR,要扣掉與n不互質的數,由於n只有兩個因數q和p,而s裡面是p的倍數有P = {p, 2p, 3p, … , (q-1)p},是q的倍數有Q = {q, 2q, 3q, … , (p-1)q},故n的RSR為s - (Q + P + {0}),所以φ(n) = pq - [(p-1) + (q-1) + 1] = pq - p - q + 1 = (p-1)(q-1)。
證明(2):p為質數,$\phi (p^k) \ \ = \ \ p^k \ \ - \ \ p^{k-1}$
此證明與上述證明蠻相向的,給定集合s = {0, 1, 2, 3, …, $p^k - 1$},由於$p^k$的因數只有p,所以要扣掉與$p^k$不互質的只要扣掉p的倍數就好,需要被扣掉的集合為P = {p, 2p, 3p, … ,$p^{k-1}p$},因此$p^k$的RSR為s - P,故$\phi (p^k) \ \ = \ \ p^k \ \ - \ \ p^{k-1}$。
證明(3):$n \ \ = \ \ p_1^{k_1}p_2^{k_2}p_3^{k_3}...p_r^{k_r}$, p is prime, then$\phi (n) \ \ = \ \ \prod_{i=1}^r \ \ p_i^{k_i-1}(p_i \ \ - \ \ 1)$
此證明結合了上述兩個證明:
Fermat’s theorem and Euler’s Generalization
Fermat’s Theorem
Let p be a prime. For every a such that gcd(a,p) = 1, then
Euler’s Generalization of Fermat’ s Theorem
For every a and n such that gcd(a,n) = 1, then
證明:定義一集合為n的RSR,{ $r_1, \ \ r_2, \ \ ... \ \ , \ \ r_{ \phi (n) }$ },則我們能利用類似compute inverse的證明,{ $ar_1 \ \ mod \ \ n,.....,ar_{ \phi (n) } \ \ mod \ \ n$ }為{ $r_1, \ \ r_2, \ \ ... \ \ , \ \ r_{ \phi (n) }$ }的重排,因此
在上述的證明中有一點值得探討,之前證明的Computing Inverse是指小於n的所有數值帶入ai mod n的話會有重牌效果,但是這邊的{ $r_1, \ \ r_2, \ \ ... \ \ , \ \ r_{ \phi (n) }$ }只包含了n的RSR,所以老師額外的證明了當a < n時此狀況還是能成立(由於之後的加密系統所用到的a都是小於n,大於n的狀況我之後有時間會去查)。由於a < n,且a與n互質,故a也是n的RSR裡的元素:
證明:Let a and b $\in$ RSR, then (a*b mod n) $\in$ RSR這邊利用反證法: