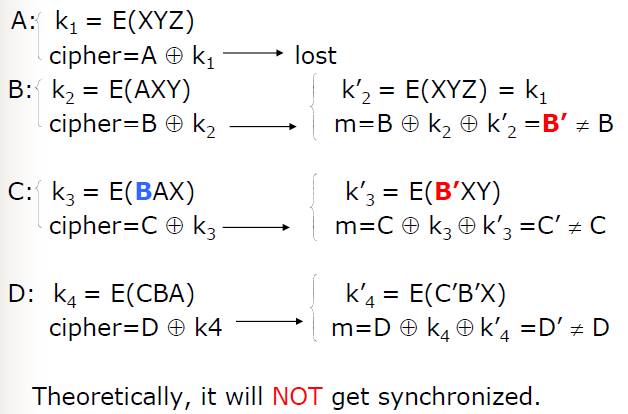Applied Cryptography-2 | Justice Shadower

來源： chapter 1 (24~28)，chapter 2 (1~22)，wiki(Lagrange polynomial)，Cracking a linear congruential generator

在前一篇提到金鑰管理，是利用方程式上的點來分散管理，那麼要如何將點還原成方程式呢？

Lagrange polynomial interpolation

定義：
給定一集合，此集合有k+1個不重複的點

$(x_0,y_0) \ \ , \ \ ... \ \ , \ \ (x_i,y_i) \ \ , \ \ ... \ \ , \ \ (x_k,y_k)$
我們定義Lagrange form為：
$L(x) \ \ := \ \ \sum_{j=0}^k y_j l_j(x)$
$l_j(x) \ \ := \ \ \prod_{0 \leq m \leq k,m \neq j} \ \ \frac{x-x_m}{x_j-x_m}$
L(x)即為此k+1個點的方程式。由於$l_j(x)$在$x=x_j$時等於1，其餘值時等於0，故：

$l_j(x_i) \ \ = \ \ \delta_{ij} \ \ = \ \ \{^{1, \ \ if \ \ j=i}_{0, \ \ if \ \ j \neq i}$
所以：
$L(x_i) \ \ = \ \ \sum_{j=0}^k y_j l_j(x_i) \ \ = \ \ \sum_{j=0}^k y_j \delta_{ij} \ \ = \ \ y_i$
故得到$L(x_i) \ \ = \ \ y_i$，此k+1個點為L(x)上的點。

Stream Cipher and Block Cipher

接下來就要進到傳統加密可怕的一堆cipher…

Methods to generate key stream (Pseudo Random Number)

傳統的SKC是利用xor來進行加密，這種加密方式key要夠亂，1跟0出現的機率要差不多，才能讓密文變的不可預測

這邊將會介紹產生亂數的方法：

Linear congruence method

$x_i \ \ \equiv \ \ ax_i \ \ + \ \ b \ \ mod \ \ m$
決定好$a$,$b$,$m$,$x_0$後，代入上述式子，{$x_i$}即為亂數。

此方法雖然看起來真的是亂數而且也無法預測，不過卻有辦法拿到亂數後計算出$a$,$b$,$m$值，進而推算出所有亂數。觀察上述式子，如果先不看$m$，而且亂數為已知的話，這是一個二元一次式，若攻擊者拿到$m$與連續3個亂數，便能計算出$a$、$b$值，因此如何拿$m$便是此攻擊的重要目標，以下介紹如何計算出$m$：

令$\ \ t_i \ \ = \ \ x_{i+1} \ \ - \ \ x_i$
令$\ \ u_i \ \ = \ \ |t_{i+2} t_i \ \ - \ \ t_{i+1}^2|$
m = gcd($u_0$, $u_1$,…, $u_k$)
當$k$越大成功$m$值正確機率越高。

證明：

$t_i \ \ = [(ax_i - b) \ \ - \ \ (ax_{i-1}-b)] \ \ mod \ \ m \ \ = \ \ a(x_i-x_{i-1}) \ \ mod \ \ m \ \ = \ \ at_{i-1} \ \ mod \ \ m$
因此$t_{i+1} \ \ = \ \ at_n \ \ mod \ \ m$，$t_{i+2} \ \ = \ \ a^2t_n \ \ mod \ \ m$
$\Rightarrow \ \ u_i \ \ = \ \ |t_{i+2} t_i \ \ - \ \ t_{i+1}^2| \ \ = \ \ a^2t_i^2 \ \ - \ \ a^2t_i^2 \ \ mod \ \ m \ \ = \ \ 0 \ \ mod \ \ m$

$u_i$為$m$的倍數，這邊探討一個問題，任意兩個$m$的倍數的最大公因數為$m$的機率是多少？這邊有個有趣的想法，任意兩個$m$的倍數可以看成$ma$、$mb$，而這兩個數又要最大公因數為$m$，意思不就是$a$與$b$要互質嗎？所以這個問題可以轉變成：任意兩個正整數互質的機率是多少？想必一些數學系的都知道答案了，這邊提供Prime Theorem 2、互質的機率兩個連結讓大家參考，裡面有證明任意兩正整數互質的機率為$(\sum_{k=1}^\infty \frac{1}{k^2})^{-1}$，其值等於$\frac{6}{\pi^2}$，大概是0.6079(關於尤拉證明的平方倒數和可以參考從調和級數到平方倒數和的意外)，而任意$n$個正整數互質的機率為$(\sum_{k=1}^\infty \frac{1}{k^n})^{-1}$，當$n$越大時其機率越接近1，所以在計算$m$時，$u_k$越多$m$值正確機率越高。

這邊再分享另外一種解法：1968年George Marsagglia提出了Random numbers fall mainly in the planes，指出linear congruential generator所產生的亂數在n維度空間下會落在少數的超平面上，Haldir運用此觀念利用linear congruential generator產生的連續四個亂數便能計算出$m$，假設此四個亂數為$a$、$b$、$c$、$d$，$m$計算方法為：

$m \ \ = \ \ \begin{vmatrix} a & b & 1 \\ b & c & 1 \\ c & d & 1 \\ \end{vmatrix}$
有關此種方法可以參考How to crack a Linear Congruential Generator。

Linear feedback shift register(LFSR)

from wiki

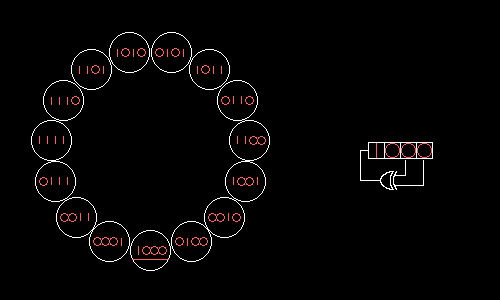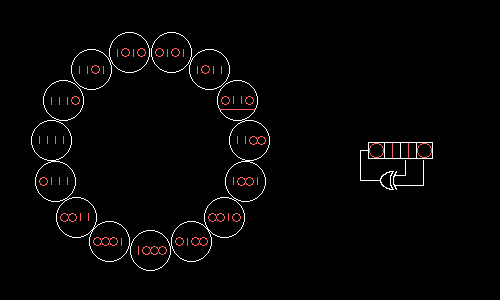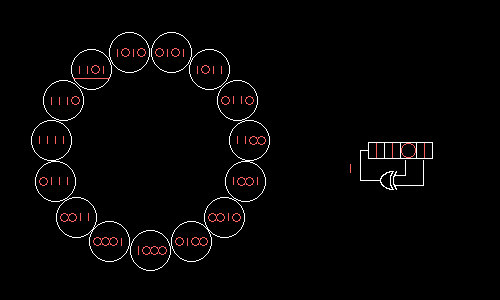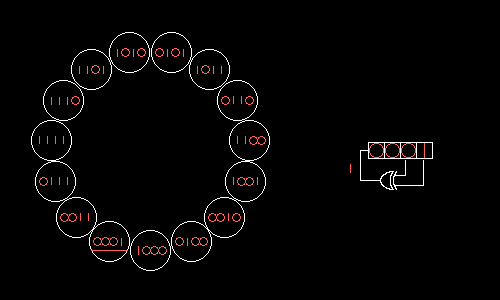
如上圖所示，這是一個4bit的LFSR，右邊電路的4bit暫存器就是我們要的亂數，他每次把右邊兩個bit拉出來做xor後，將暫存器往右shift一個bit，並將xor結果放到最左邊的bit，注意左邊的15個狀態，除了0000其餘都有在上面，因為只要出現全0之後狀態就都是0了 (0 xor 0 = 0)。在這張圖上是拉最後兩bit，那要如何知道拉哪些bit會讓亂數最亂呢？

The max period of LFSR

當一串數為亂數時，代表此串亂數不可預測，既然不可預測那這串數就沒有週期，換句話說這串數的週期為無限大。所以這邊要討論如何讓LFSR的週期最大。設定$b_n$為二進位數，當第n個bit要拉下來作xor時，$b_n$為1，反之不拉下來時$b_n$為0，$b(x) \ \ = \ \ b_4x^4 \ \ + \ \ b_3x^3 \ \ + \ \ b_2x^2 \ \ + \ \ b_1x \ \ + \ \ 1$，如果$b(x)$是primitive多項式，則此LFSR週期最大，可產生m-sequence。
(Primitive polynomial之後上課會證明)

cryptanalysis(可預測)：LFSR若長度為n，則已知2n個連續output就可以得知後續所有($2^n$-1-2n)個output，解N元一次方程式。

由於有上述預測攻擊，後來就有利用Nonlinear mapping的方法產生PN sequence。

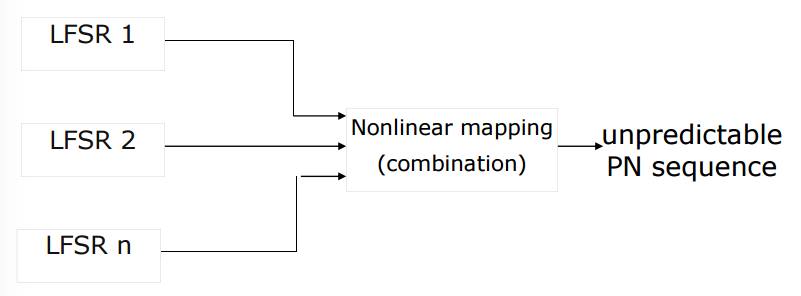
PN Sequence Generator

Stream Cipher

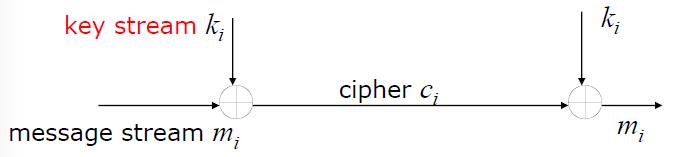
有了LFSR基本觀念後，接下來我們利用它所產生的PN sequence來接stream cipher。Stream Cipher主要精神為與明文做XOR的key每個bit都不同，明文有多少個bit就需要產生多少個亂數bit來做XOR，因此如果要連續的產生亂數，就必須要有源源不絕的seed，這邊會介紹三種mod，分別是output feedback mode(OFB)、counter mode、cipher feedback mode(CFB)。

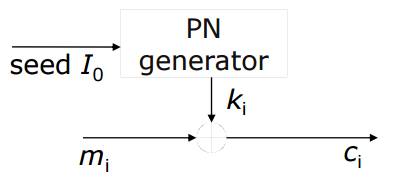
利用PN sequence產生亂數與明文做XOR

Output Feedback Mode (OFB)

Output feedback mode主要是把產生出來的亂數取一個bit當作key，然後將結果當作下一次的seed，此種模式可以不受error propagation影響，如果有某個bit在傳送過程中出錯，接收方只會在此bit解錯，其餘bit能夠正常解回來，但如果傳送途中有發生bit loss，則會失去同步。

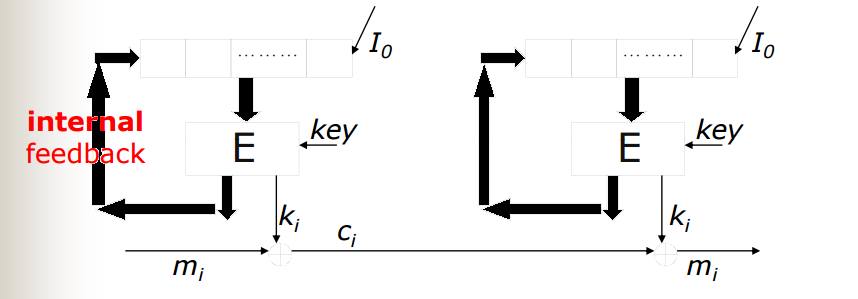
Output Feedback Mode

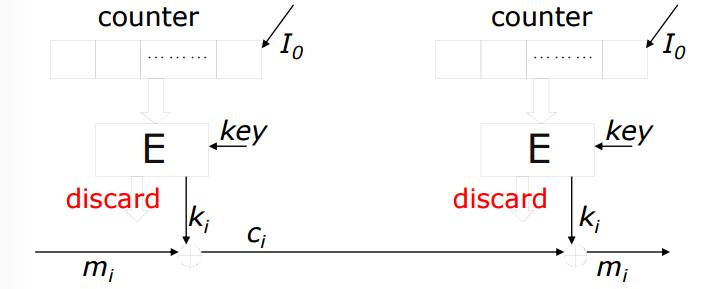
Counter Mode

counter mode 的seed為一個counter，此方法好處為能夠自由控制你要解第幾個bit，只要輸入正確的counter就好了，如果考慮到安全的話，E所設計的亂數要夠亂，假設輸入兩種input只差一個bit，通過亂數產生出來的亂數應該要差超過兩個bit以上，輸入與輸出應該毫無關係，這樣才是一個好的亂數設計。但此方法如果要做到random access，必須先知道要access第幾個bit，直觀上也不大方便。

Counter Mode

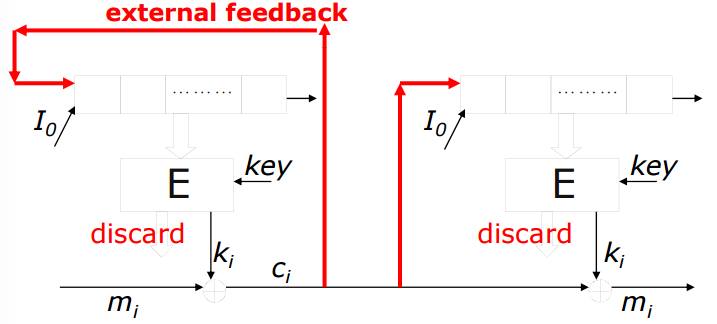
Cipher Feedback Mode (CFB)

Cipher feedback mode能夠實現自我同步，當傳送過程中發生error propagation或是bit loss，都能在經過一個register的大小後自我同步回來。他是將XOR後的cipher當作seed傳回register的第一個bit，當你要access第m個bit時，只要將m的前n個(register size)cipher當作seed便能正確取得key，不用像counter mode需要知道第幾個。

Cipher Feedback Mode

下圖為cipher bit “A” lost時發生的狀況，圖中可以看到lost後有三個register狀態是亂掉的情況(register size為3)，但之後register又同步了。

Question ： Message Feedback Mode 能夠自我同步嗎？

既然cipher是depend on message，那message feedback mode應該也可以自我同步囉？

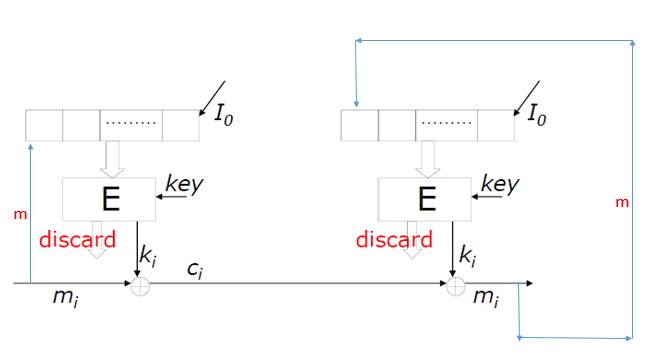
Message Feedback Mode

當然不行！仔細想想，如果拿message來當作feedback，那麼傳送途中發生任何錯誤，解出來的message也會是錯誤的，此時register會在繼續解下一個進來的cipher，但就算下一次的cipher是正確的，register已經錯誤了，故解回來的message並不會是正確的，因此只要錯了一個bit後，基本上以後的所有bit都毀了。下圖為message feedback mode 的實際例子。