上禮拜最後講中國餘數定理,可以將大世界的複雜計算分給很多個小世界,小世界計算完後透過中國餘數定理merge回來,接下來的二次剩餘將會運用到中國餘數定理。
Quadratic Residues
Quadratic Residues探討在模數世界開根號的問題,既然是開根號就分為兩種:可以開根號跟不能開根號。
- Quadratic Residue ($QR_p$)
定義p為質數,若某數平方後mod p能找到a,則我們稱a為$QR_p$:$x^2 \ \ \equiv \ \ a \ \ (mod \ \ p)$ - Quadratic Nonresidue($NQR_p$)
若mod p底下有一個數a,他找不到任何x使得$x^2 \ \ \equiv \ \ a \ \ (mod \ \ p)$,則代表a在mod p底下不能開根號,稱為$NQR_p$。
知道了在模數底下分為可開根號跟不可開根號後,接下來我們來看看在mod p底下(p為質數),會有多少個$QR_p$跟$NQR_p$呢?mod p 底下總共會有0~p-1共p個數,0在這邊暫且不談,我們將其他的數都做平方來觀察:
觀察$1^2$跟$(p-1)^2$,這兩數平方後mod p都是1,所以1的平方根為1跟p-1,其他數也是如此,其實如果把p改成0就是我們平常認知的平方根了,所以k根p-k一組,剛好從中間切半,那左半邊的平方後mod p會不會有兩個根對到同一個數呢?下面利用反證法來證明:
假設$x^2 \ \ \equiv \ \ a \ \ \equiv \ \ y^2 \ \ (mod \ \ p)$,且x,y不相等,$1 \ \ \leq \ \ x,y \ \ \leq \ \ \frac{p-1}{2}$,則x不是跟y一樣就是p-y,但這兩種都不符合條件,因此平方根不會同時有兩個小於(p-1)/2,也就是在小於(p-1)/2的情況下會有兩個數平方後mod p會是同一個數。
接下來說明如何區分$QR_p$跟$NQR_p$:
proof:
先驗證$y^{ \frac{p-1}{2}}$ mod p是否只會有1跟-1兩種結果:假設$y^{ \frac{p-1}{2}}$ mod p = t,則
$$t \ \ \equiv \ \ y^{ \frac{p-1}{2}} \ \ (mod \ \ p) \\ \Rightarrow t^2 \ \ \equiv \ \ y^{ p-1} \ \ (mod \ \ p) \\ \Rightarrow t^2 \ \ \equiv \ \ 1 (mod \ \ p)$$
因此t確實只有正負1。接下來為什麼mod p後等於一就是$QR_p$了呢?假設y是a的平方根,則
$$y \ \ \equiv \ \ a^2 \ \ (mod \ \ p) \\ \Rightarrow \ \ y^{ \frac{p-1}{2}} \ \ \equiv \ \ a^{p-1} \ \ (mod \ \ p) \\ \Rightarrow \ \ y^{ \frac{p-1}{2}} \ \ \equiv \ \ 1 \ \ (mod \ \ p)$$
所以剩下的$NQR_p$就是等於-1了。
Legendre symbol
接下來利用剛剛$y^{ \frac{p-1}{2}}$ mod p的特性我們定義Legendre symbol:
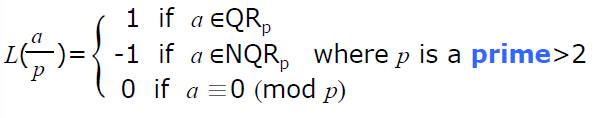
由於剛剛我們沒有把0討論進去,這邊0不算$QR_p$也不算$NQR_p$,之後密碼學也不太會用到就不管他XD這邊要注意的是p最小是3,等於二的話套入剛剛式子就變成$y^{1/2}$了。
Characteristic of $QR_p$ and $NQR_p$
$$QR_p \ \ \times \ \ QR_p \ \ \rightarrow \ \ QR_p \\ QR_p \ \ \times \ \ NQR_p \ \ \rightarrow \ \ NQR_p \\ NQR_p \ \ \times \ \ QR_p \ \ \rightarrow \ \ NQR_p \\ NQR_p \ \ \times \ \ NQR_p \ \ \rightarrow \ \ QR_p$$
這邊就跟國中教的正正得正負正得負一樣了…兩個$QR_p$相乘還是$QR_p$,一個$QR_p$跟$NQR_p$相乘會變成$NQR_p$這些都比較好理解,因此這邊來說明一下”負負得正”:給定兩個$NQR_p$為X跟Y,則:
$$X^{ \frac{p-1}{2}} \ \ \equiv \ \ -1 \ \ (mod \ \ p) \ \ and \ \ Y^{ \frac{p-1}{2}} \ \ \equiv \ \ -1 \ \ (mod \ \ p) \\ \Rightarrow \ \ (X \ \ \times \ \ Y)^{ \frac{p-1}{2}} \ \ \equiv \ \ X^{ \frac{p-1}{2}} \ \ \times \ \ Y^{ \frac{p-1}{2}} \ \ (mod \ \ p) \\ \Rightarrow \ \ (X \ \ \times \ \ Y)^{ \frac{p-1}{2}} \ \ \equiv \ \ -1 \ \ \times \ \ -1 \ \ \equiv \ \ 1 \ \ (mod \ \ p)$$
Jacobi symbol
如果遇到的模數不是質數而是合成數的話,可以將合成數拆成質數後再去算Legendre symbol,下列為Jacobi symbol Properties:
$$J( \frac{a}{pqr}) \ \ = \ \ L( \frac{a}{p}) \ \ \times \ \ L( \frac{a}{q}) \ \ \times \ \ L( \frac{a}{r}) \ \ p,q,r \ \ \in \ \ odd \ \ prime \\ J( \frac{a_1*a_2}{n}) \ \ = \ \ J( \frac{a_1}{n}) \ \ \times \ \ J( \frac{a_2}{n})$$
這邊要注意的是,如果要使 $a \ \ \in \ \ QR_n$,則a必須是所有n的質因數的QR才行,剛剛講的QR跟NQR特性是在同一個質數的模數底下,這邊用Jacobi symbol拆開的模數是不同的質數。這邊舉個例子:
假設要算$J( \frac{a}{pq})$ ,如果$J( \frac{a}{p})$ 與$J( \frac{a}{q})$ 都是-1,則不能像剛剛那樣(-1)*(-1)=1,因為這邊模數一個是p一個是q,因此只要有一個Jacobi symbol值為-1則a就是NQR。
講了這麼多數論的東西,終於要進到第一個實際運用的系統了(灑花~~),繼續講數論的話很多同學可能看到數學就…

好啦回歸正題,我們可以運用剛剛的QR以及NQR來設計一個帳密系統,這個帳密系統只能在local端登入,並且使用者去註冊時帳號密碼都是系統給你的,使用者無從選擇。帳號密碼管理通常就是建一張表格,表格內容每個entry就是一組帳號對應到密碼,如果要安全一點的可能把密碼丟進hash存hash值。這邊我們可以利用QR跟NQR來儲存帳號相對應的密碼,而且密碼只需要存2個bit就夠了。
這系統既然會用到QR跟NQR,那他就一定是要開根號囉?沒錯,這系統主要運作原理就是選定一個帳號,然後將帳號開根號後得到密碼,丟給使用者,那麼你一定會問,如果密碼是把帳號開根號,那我自己開根號就好了啊,有帳號不是就等於有密碼了?這邊的關鍵點就在模數底下對合成數的開根號。現今在這世上對合成數開根號的演算法是利用中國餘數定理,把合成數拆成質數分別做開根號,如果不用中國餘數定理做的話就跟暴力法沒兩樣了,所以我們能利用這點,設計一個合成數n,n為兩個質數p,q相乘,n能公開但p跟q不公開,將帳號在mod n底下開根號得到密碼,如此一來攻擊者如果不知道如何將n拆成p跟q,那麼他也無法將帳號做開根號的動作來得到密碼了。有了這概念後接下來問題來了,你說要在模數底下開根號,可是我們剛剛才講過,開根號的世界可以分成QR跟NQR,並不是所有數都能開根號啊,所以接下來系統裡面會有一張表,這張表就是來處理這問題,讓所有帳號進來都能夠被開根號。
那這張表到底有什麼神奇魔力能夠讓NQR也可以開根號?其實就是用剛剛講到的QR跟NQR的特性,就是那個國中講的負負得正啦!如果今天帳號進來是NQR,那就讓他在乘上一個NQR不就可以開根號了~接著我們來詳細介紹這張表的內容:

首先n = pq剛剛有講過,然後mod p可以分為QR跟NQR,mod q也能分為QR跟NQR,所以pq組合起來會有四種,後面的-1表示NQR,+1表示QR,如此一來帳號在mod n底下的所有可能性都在這張表上面了,然後我們在這四種狀況分別找一個數,就是前面的$ \alpha \ \ \beta \ \ \gamma \ \ 1$。接著我們來看管理者要如何儲存帳號跟密碼:
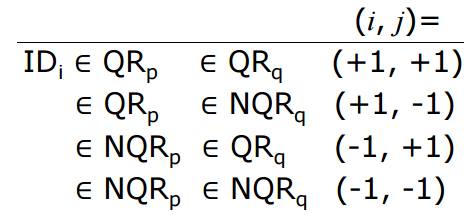
帳號(ID)在mod n底下也會是那四種可能的其中一種,所以密碼就記錄對p是+1還是-1,對q是+1還是-1,因此密碼欄位只需要兩個bit。有了上面這兩張表後,當我選定了一個ID,對應到密碼欄位(i.j)得知他的QR、NQR狀態,再去剛剛的表格看要選$ \alpha \ \ \beta \ \ \gamma \ \ 1$哪一個k來跟帳號相乘,如此一來相乘結果就能開根號了。下表是將剛剛講的兩張表結合整理:
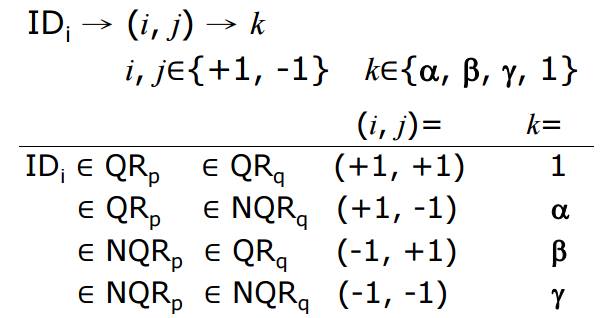
- Password generation:
$$(Pw_i)^2 \ \ \equiv \ \ ID_i \ \ \times \ \ k \ \ (mod \ \ n) \ \ n \ \ = \ \ p*q \\ (choose \ \ the \ \ smallest)$$
注意這邊ID開根號完會有4個密碼,因為是在mod合成數底下造成的,mod一個質數開根號後會有兩個根,我們設定的n擁有兩個質數,因此密碼會有四個根,至於為什麼要選擇最小的則是因為攻擊者如果拿到這四個根,他就有辦法解出p跟q,詳細狀況待會說明,先來看看這四個根如何解。
要解合成數的開根號當然是運用中國餘數定理,將原本mod n底下拆成mod p跟mod q,分別計算出根號值之後再merge回來。下圖為示意圖:
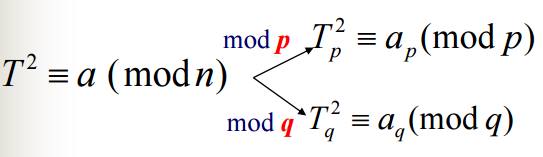
$a_p$開根號後假設值為$S_1$, p-$S_1$,$a_q$開根號後為$S_2$, q-$S_2$,而T在mod n底下的四個值假設為x, n-x, y, n-y,則x會是$S_1$跟$S_2$ 利用中國餘數定理merge而成,n-x會是 p-$S_1$ 跟 q-$S_2$ merge而成,同理y會是$S_1$跟 q-$S_2$ merge,n-y是$S_2$跟 p-$S_1$ merge。簡單來說就是兩兩成對,四個根會有兩對pair。基本上到目前為止整個帳密系統輪廓都描繪出來了,就還差一個細節,記得剛剛講說利用中國餘數定理將合成數拆成質數,然後就能計算出開根號,那mod 質數底下要怎麼找開根號的兩個根呢?在1891年Alberto Tonelli發展了一個演算法解決了這問題,但此演算法效能不佳,在1973年Daniel Shanks發展了Tonelli–Shanks algorithm,也就是接下來要講的演算法。
Tonelli–Shanks algorithm
此演算法要解決的問題如下:p為質數,n為$QR_p$,找出x使得
其實Joseph-Louis Lagrange有找到當$p \ \ \equiv \ \ 3 \ \ (mod \ \ 4)$情況下,$x \ \ \equiv \ \ \pm n^{ \frac{p+1}{4}}$ (from wiki),會說明這個特殊狀況是因為待會演算法裡面有這個…
Algorithm:
Input : p, n,p為odd prime,n為integer且$QR_p$
Output : R, $R^2 \ \ \equiv \ \ n \ \ (mod \ \ p)$
步驟一:將p-1所有2的因數除掉,除到最後為奇數Q,令S為2的個數:$p \ \ - \ \ 1 \ \ = \ \ Q \ \ * \ \ 2^S$,當S=1時return $\pm n^{ \frac{p-1}{4}}$ (剛剛講的特殊狀況)
步驟二:選擇一個z使得z為$NQR_p$,並且令$c \ \ \equiv \ \ z^Q \ \ (mod \ \ p)$
步驟三:令$R \ \ \equiv \ \ n^{ \frac{Q+1}{2}} \ \ (mod \ \ p), \ \ t \ \ \equiv \ \ n^Q, \ \ M \ \ = \ \ S$
步驟四:Loop:
- if t $ \equiv $ 1 (mod p),return R
- 找到最小的i,0 < i < M,使得$t^{2^i} \ \ \equiv \ \ 1 \ \ (mod \ \ p)$
- $b \ \ \equiv \ \ c^{2^{M-i-1}}, \ \ R \ \ \equiv \ \ bR, \ \ t \ \ \equiv \ \ tb^2\ \ (mod \ \ p)$, M = i
證明:
其實只看演算法會看到霧煞煞,我們來整理一下:看一下步驟四的迴圈,當t=1時回傳R,因此我們可以知道R就是根號n,那跟t=1有什麼關係?由於我們設定$R \ \ \equiv \ \ n^{ \frac{Q+1}{2}} \ \ (mod \ \ p), \ \ t \ \ \equiv \ \ n^Q$,因此$R^2 \ \ \equiv \ \ nt \ \ (mod \ \ p)$,所以當t=1時R為n的平方根。那t什麼時候才會變成1呢?說明這個之前先補充一個預備知識:order,給定$m \ \ \in \ \ N, \ \ a \ \ \in \ \ Z$,滿足gcd(a,m)=1,若$n \ \ \in \ \ N$是最小正整數滿足$a^n \ \ \equiv \ \ 1 \ \ (mod \ \ m)$,則稱n為a在mod m底下的order,並以$ord_m(a) \ \ = \ \ n$表之。(參考基礎數論)
接著我們看步驟二的c,由於$c \ \ \equiv \ \ z^Q \ \ (mod \ \ p)$,因此$c^{2^S} \ \ \equiv \ \ (z^Q)^{2^S} \ \ \equiv \ \ z^{Q2^S} \ \ \equiv \ \ z^{p-1} \ \ \equiv \ \ 1 \ \ (mod \ \ p)$,此時還不確定$2^S$就是c的order,因此我們檢查$2^{S-1}$:$c^{2^{S-1}} \ \ \equiv \ \ z^{ \frac{p-1}{2}} \ \ \equiv \ \ -1 \ \ (mod \ \ p)$,最後的等於-1是Legendre symbol,由此可知c的order為$2^S$。
接下來是關鍵的t,雖然$t^{2^S} \ \ \equiv \ \ 1 \ \ (mod \ \ p)$,但由於c是利用z是NQR來讓$c^{2^{S-1}}$算出來結果是-1,t在這邊無法如法炮製,因此我們假設t的order為$2^{S’}$。接著我們為了讓下一回合保持$R^2 \ \ \equiv \ \ nt \ \ (mod \ \ p)$,在步驟四中設定了$b \ \ \equiv \ \ c^{2M-i-1}, \ \ R \ \ \equiv \ \ bR, \ \ t \ \ \equiv \ \ tb^2 \ \ (mod \ \ p)$,如此一來就可以看成$(bR)^2 \ \ \equiv \ \ n*b^2*t \ \ (mod \ \ p)$,$b^2$消掉的話就跟原式一樣。
接著我們看一下c’,$(c')^{2^{S'}} \ \ \equiv \ \ b^{2^{S'} \ \ * \ \ 2} \ \ \equiv \ \ b^{2^{S'+1}} \ \ \equiv \ \ c^{2^{S-S'-1+S'+1}} \ \ \equiv \ \ c^{2^S} \ \ \equiv \ \ 1 \ \ (mod \ \ p)$,這邊就可以了解S-S’-1的-1是為了消掉後面的平方,-S’是為了後來要讓$2^{S’}$消掉,而$(c')^{2^{S'-1}} \ \ \equiv \ \ c^{2^{S-1}} \ \ \equiv \ \ -1 \ \ (mod \ \ p)$,故c’的order為$2^{S’}$。
這邊先來整理一下思緒,我們剛剛假定t的order為$2^{S’}$,然後推導到後來c’居然order也一樣是$2^{S’}$,由此可知下一輪的t’跟c”會有S” < S’,而他們的order為$2^{S”}$。所以當S”為0時,$2^{S”}$ = 1,也就是說$t^{2^{S"}} \ \ \equiv \ \ t^1 \ \ \equiv \ \ 1 \ \ (mod \ \ p)$,我們最想看到的t=1終於出現了,如果S”不為0沒關係繼續下一輪,因為S只會越來越小,所以當最後t找不到order時,t的次方選項就剩下0可以選了,此時的R即為根號解。
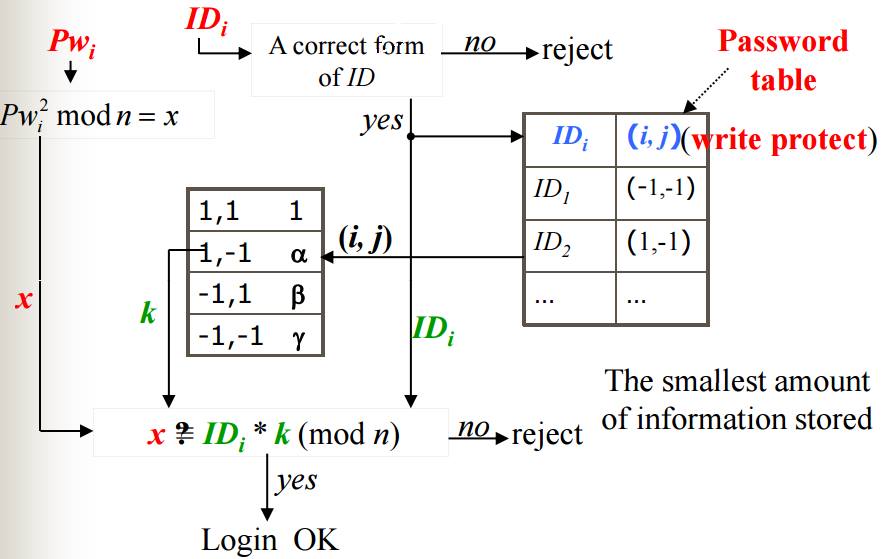
上圖為系統登入流程,使用者輸入帳號密碼後,確認帳號存在查帳密那張表,密碼部分紀錄的是(i,j),再去找k來跟ID相乘,最後結果再與密碼平方來做比對,便能得知帳密是否正確了。接著來說明剛剛算出的四個根當中要選固定的給使用者,以剛剛四個根x, n-x, y, n-y為例,如果攻擊者拿到x或n-x與y或n-y的話,攻擊者就有1/2的機率計算出p跟q了。
假設ID在mod p底下算出來的答案是$S_1$, p-$S_1$,在mod q底下算出來的答案是$S_2$, q-$S_2$,利用中國餘數定理將$S_1$, $S_2$計算出密碼得到x,$S_1$, q-$S_2$計算出密碼得到y,而攻擊者拿到的密碼為x跟y,則:
gcd(x+y, n) = q
gcd(x-y, n) = p
計算出最大公因數居然就能得到pq,這邊分析一下x跟y。
$$x \ \ \equiv \ \ S_1 \ \ (mod \ \ p) \\ x \ \ \equiv \ \ S_2 \ \ (mod \ \ q) \\ y \ \ \equiv \ \ S_1 \ \ (mod \ \ p) \\ y \ \ \equiv \ \ -S_2 \ \ (mod \ \ q) \\ therefore \\ x+y \ \ \equiv \ \ 0 \ \ (mod \ \ q) \\ x-y \ \ \equiv \ \ 0 \ \ (mod \ \ p)$$
所以只要四個根都知道的話就能拿不同pair的密碼來破解pq了。
接著我們看另外一種情境:假設帳號是使用者可以決定,而且儲存帳密的表被攻擊者拿到而且有寫入的權限,那麼攻擊者就能夠自己設定密碼,將密碼平方後mod n,此數即為帳號,之後在將表格的密碼欄位寫為(1,1),此時系統在查要與帳號相乘的數就會是1,因此攻擊者就可以自行創造帳號與密碼了。
上述情境是在ID可易讓使用者選擇,而且帳密的表可以被寫入,那麼如果儲存帳密的表不能寫的情況,ID還是可以讓使用者自行選擇,還有辦法攻擊嗎?這題老師明講了是其中考題。(其中考過了~補上解答)
Rabin Encryption V.S. RSA
QR跟NQR的概念應用在Rabin Encryption,加密時將明文平方變為密文,解密時開根號回來為明文,安全性一樣是落在將合成數拆成兩質數相乘。
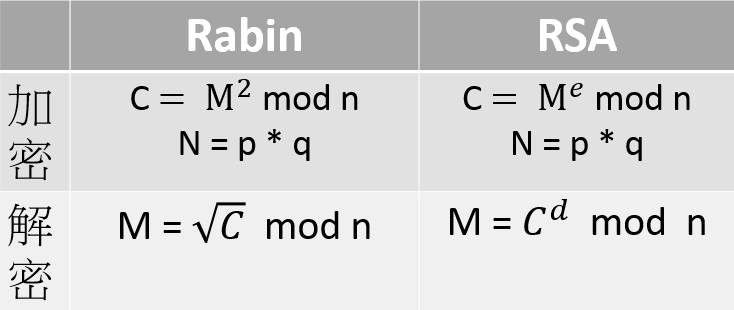
上圖是兩個演算法加解密比較,過程看起來蠻類似的,如果要在比較小運算能力比較差的機器上做加密的話,可以選擇Rabin,因為他加密只需要做平方跟mod;而數位簽章的話剛好跟加解密反過來,因此如果要驗證簽章是否正確的話Rabin適合在計算能力較差的device上。
Generator
定義:If p is a prime and g is less than is less than p, then g is a generator modulo p if for all 1 ≤ m ≤ p-1, $\exists \ \ a \ \ \in \ \ g^a \ \ \equiv \ \ m \ \ (mod \ \ p)$
簡單來說就是把generator當底數,他的次方在小於p的所有指數mod p後可以將所有小於p的數創造出來。下面就是mod 11底下以2為generator:
