來源:chapter 3(50 ~ 54),chapter 4(1 ~ 18)
Primitive Root
上禮拜有講到generator的概念,剛好我自己補充的東西也有提到order的概念,這邊會統整一下所有的概念。
Theorem: If λ is the order of α, then λ|(p-1).
proof: 這邊利用反證法,令 λ 不是p-1的因數,則 p-1 = t*λ + k,1≤ k ≤ λ −1,則:
得到 k < λ,$\alpha^{k} \ \ \equiv \ \ 1 \ \ (mod \ \ p) \ \ \rightarrow \leftarrow$得證。
給定一正整數n,n的RSR(Reduced set of residues)標記為$Z_{n}^{*}$,若a的次方mod n底下能夠產生$Z_{n}^{*}$的所有元素,也就是a為$Z_{n}^{*}$集合的generator,則我們稱a為n的Primitive Root。而$Z_{n}^{*}$的個數尤拉定義為φ(n),因此如果a為n的Primitive Root,則a必須產生所有的$Z_{n}^{*}$,也就是說a的order必須為φ(n),如果a的order比φ(n)小的話,代表a的次方還沒到達φ(n)就已經是一個周期了,此時不可能產生出$Z_{n}^{*}$集合的所有元素。下圖是摘錄自wiki,圖中可以看到n選的數為14,3跟5都能夠將14所有的RSR產生出來,因此3跟5為14的primitive root:
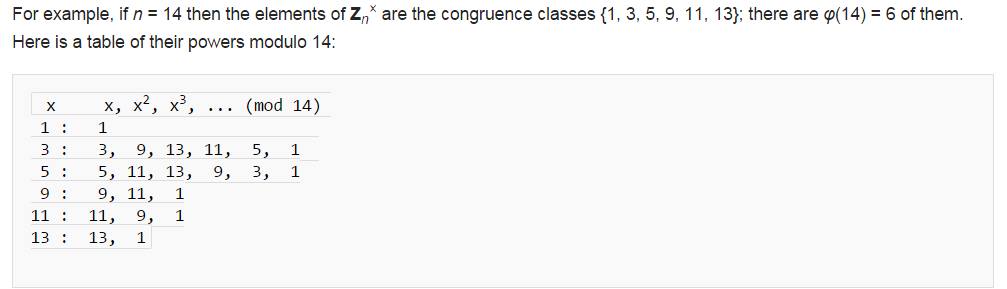
這邊值得注意的是,並不是所有的正整數n都能夠找到primitive root,像剛剛wiki裡面就有舉例子,15就會找不到primitive root了。那麼如果是有primitive root的數,那麼這個數的primitive root會有幾個?這邊查了一下蠻多文獻都寫(Burton 1989)但是都查不到證明….n的primitive root個數為φ(φ(n))。在之後的密碼系統會用到的是質數居多,這邊我就以p來表示質數,因此的primitive root個數就是φ(p-1),從這邊可以看得出來質數的generator還蠻多的,不用怕找不到。
接下來介紹老師51頁投影片紅色框框的式子,這邊我用wiki上的Eulers totient function來介紹。這式子是由高斯所發現的,他發現正整數可以用尤拉函式的和來表示:
Divisor sum:
這式子乍看之下蠻神奇的,也就是說把n的所有因數經過totient function後的總和會得到n。這邊我用n=10來舉例子,我將0~1切成10等分,所有的分數形式如下:
接著我們約分:
到這邊可能還有點模糊,我們將上列數字依照分母分類然後由小排到大:
有沒有發現一件神奇的事情,分類完後分母就是10的因數,分子是分母無法整除的數(廢話嗎不然怎叫約分),既然如此上面不就可以表示成各個因數的totient function總和了?理解完畢後老師的投影片的式子就比較容易理解:

接著來看在mod 質數p之下如何找出generator:剛剛有講過generator的特性,假設g為p的generator,則g的order必須為φ(p),也就是說g的次方在p-1之前都不能等於一,利用這一個特性我們可以在小於p的所有數都拿來測,只要他一次方兩次方三次方到p-2次方都不為一,只有在p-1次方mod p等於一時就是generator了。
不過這麼做好像有點暴力,我們剛剛有一個理論是” If λ is the order of α, then λ|(p-1). “,這樣就好辦多了,既然order只會發生在p-1的因數裡面,那我們只需要檢查p-1的因數就行了。至於該如何檢查p-1的因數呢?這邊可以不用每一個因數都試,舉個簡單的小例子:假設p-1 = abc,那我們只需要測ab,bc,ac這三個看看這些次方會不會等於一就好了。因為如果$g^{ab}$ mod p不等於一,那麼$g^{a}$跟$g^{b}$都不會等於一了,以此類推,但相反的如果只測試a,b,c這三個,那麼有可能$g^{a}$跟$g^{b}$都不是1,但是$g^{ab}$卻是1這種狀況。
接著我們看實際的演算法,用剛剛的例子套用到這上面來看的話,他每次就是挑掉一個因數,然後測試其餘的乘積的次方是否為一:

有了這個演算法後我們就能找出質數p的generator了~但是實際上並沒有這麼順利,在現實生活中p是個很大的質數,所以要將p-1做質因數分解是很難的,那我們剛剛不就白解了嗎….實際運用上通常都是設定p-1等於兩倍的令一個質數,這樣質因數分解就是2跟剛剛設定的質數,之後會講到如何製造質數。
Introduction to Public-Key Cryptography
終於要進到近代密碼系統了,近代密碼系統主要精神就是將資訊透過現階段的難題進行編碼,但這難題可以透過知道某些key information進而變為簡單的題目。下面將舉一個Knapsack problem來當例子:
Knapsack problem
聖誕節快到了,聖誕老公公招集了一群小朋友到一間禮物房,裡面擺滿了各式各樣的禮物。在這間房間裡的每一個禮物上面都貼著一個標籤,上面寫著該禮物的重量,每個禮物重量都不相同。此時聖誕老公公拿了一個大袋子裡面裝滿了東西,他說:「這裡面都是你們在這間房間看的到的禮物,而且裡面並不會有重複一樣的禮物。但我只會告訴你們這個大袋子裡面裝的東西的總重量,如果有哪個小朋友知道這裡面總共有哪些禮物,那你就能得到這一袋」。
突然覺得這個聖誕老公公有點壞心…其實這就是一個Knapsack problem,當然他還有其他很多種變型,這邊我們要用的是:知道總重量求個別物品。我們可以設計一個長度為t的亂數陣列,在這陣列當中取m個的總和,這時如果要將這m個總合求原本是哪些亂數就變成了Knapsack problem。那Knapsack problem要如何運用到加密呢?我們可以設計取m個的總和的取法就是message,那他們的總和就是密文。
given $(r_t, \ \ r_{t-1}, \ \ ... \ \ , \ \ r_1, \ \ r_0)$ and $(m_t, \ \ m_{t-1}, \ \ ... \ \ , \ \ m_1, \ \ m_0)$ r就是剛剛講的亂數陣列,m就是取法,m為bit 陣列,$m_n$為1代表$r_n$要選,為0代表$r_n$不選。
因此 $C \ \ = \ \ \sum_{i=0}^{t} r_i \ \ \times \ \ m_i$ C為密文,C非常容易計算出來,但是要從C推回m是個難題。但如果從C推回m為難題對於解密方不就也是難題了?因此我們必須設計一個key information來讓解密方知道key之後就不是難題:設計 $r_i \ \ = \ \ 2^i \ \ \times \ \ K \ \ mod \ \ p \ \ (where \ \ p \ \ \geq \ \ 2^{t+1} )$,K就是key,對於知道key的人來說,這個亂數陣列的組合就會變成將C從十進位轉為二進位表示,因為亂數都是2的次方,那不知道K的人這問題依舊是一個難題。
而利用Knapsack problem來製造一個function使得計算總合容易,但從總合推算回去很難,這種function稱為one-way function。但我們可以利用一個key來讓此問題變簡單,這就好像多了一道暗門一樣,只有知道內線消息(key)的人才有辦法通過。
近代密碼系統就是建立在理論上解的出來,但計算上所耗費的時間成本會讓人不想去解這密碼,因此之後的量子電腦出現後很多的難題對他來說都變成簡單的題目,而加解密又是建立在這難題之上,所以量子電腦出現後可能密碼世界會再被改寫也不一定…
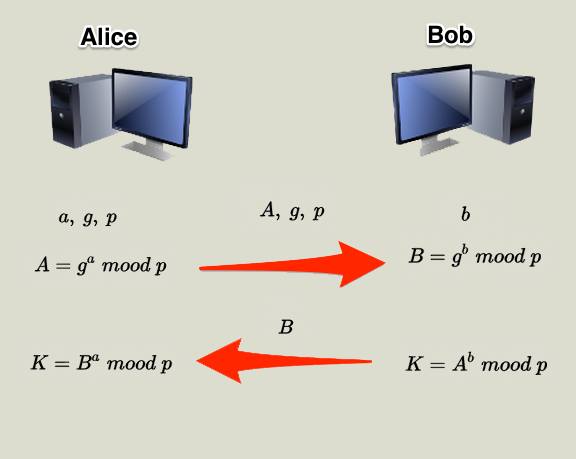
而最早被公開的近代密碼系統莫過於Diffie-Hellman Public Key-Exchange了,在第一章節有講過其細節,Diffie-Hellman利用了離散對數難題來進行金鑰交換。雖然這演算法是安全的,但無法抵禦man-in-the-middle attack:
首先先來看正常情況,Alice將A,g,p傳給Bob,Bob將B傳給Alice,雙方計算完後得到共同的key K(細節請看之前的Applied-Cryptography-1),如下圖(來源:stackoverflow):
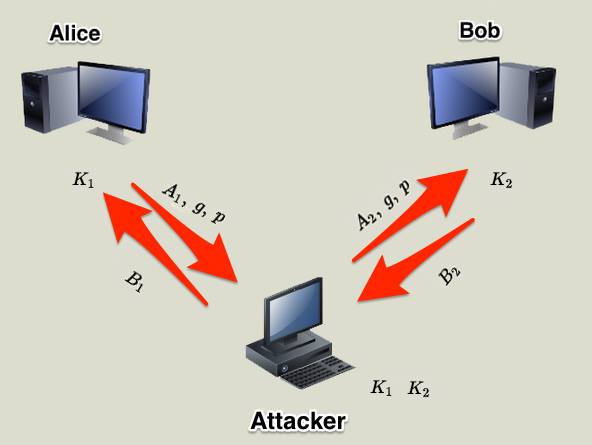
接著我們看man in the middle attack,顧名思義就是中間有一個人在攻擊,當Alice要傳給Bob資訊時,中間的攻擊者將資訊攔截下來,並且自己位裝成Bob計算出$B_1$給Alice;同時再偽裝成Alice傳$B_2$給Bob,這時攻擊者就擁有了跟Alice通訊的$K_1$與跟Bob通訊用的$K_2$,如下圖:
接著我們用學過數論的角度來看RSA,相信RSA演算法大家都蠻熟的了,這邊直接看加解密過程:
Encryption:
Decryption:
$$m \ \ \equiv \ \ C^d \\ \equiv \ \ m^{ed} \ \ (mod \ \ n) \\ \equiv \ \ m^{1+k \phi (n)} \ \ (mod \ \ n) \\ \equiv \ \ m \\ (where \ \ e \ \ \times \ \ d \ \ \equiv \ \ 1 (mod \ \ \phi (n)))$$
這邊可以看到用到尤拉的式子使$m^{ \phi (n)}$在mod n底下為1。那這個式子需要建立在m跟n互質的情況下才成立,那這時候就出現問題了,我的message一定會跟n互質嗎?我們來看看m跟n不互質的機率是多少。在mod n底下總共有n-1個數,其中有φ(n)個數與n互質,而在RSA演算法中n為兩個很大的質數相乘,令n = pq,則m跟n不互質機率為:
假設pq都是512bit的質數,則:
這個數應該能夠看成趨近於零了吧….那如果就是這麼剛好遇到跟n不互質的數那就完了嗎?這邊RSA非常神奇的還是能夠解的回來。如果m跟n不互質,那m一定是p的倍數或是q的倍數,而且不可能同時是p跟q的倍數,因此假設m = ap,且gcd(a,q) = 1(因為q為質數且a不可能為q的倍數),我們利用中國餘數定理將m分散到p跟q兩個小世界裡:
$$m \ \ mod \ \ p \ \ = \ \ 0 \\ m \ \ mod \ \ q \ \ = \ \ ap \ \ mod \ \ q$$
接著進行加密: $C \ \ = \ \ m^e \ \ mod \ \ n$
$C \ \ \rightarrow \ \ (0^e \ \ mod \ \ p, \ \ (ap)^e \ \ mod \ \ q)$
解密:
$$C^d \ \ mod \ \ n \rightarrow \ \ (0^e \ \ mod \ \ p, \ \ (ap)^{ed} \ \ mod \ \ q) \\ = \ \ (0, \ \ (ap)^{1+k \phi (n)} \ \ mod \ \ q) \\ = \ \ (0, \ \ (ap)^{1+k(p-1)(q-1)} \ \ mod \ \ q) \\ = \ \ (0, \ \ (ap) \ \ \times \ \ [(ap)^{(q-1)}]^{k(p-1)} \ \ mod \ \ q) \\ = \ \ (0, \ \ (ap) \ \ mod \ \ q) \\ = \ \ m$$
太神奇了,在m跟n不互質狀況下居然解的回來,這邊是因為雖然在原本大的世界n是不互質的,但是到了小世界p跟q之後一個變成0一個依然是互質,所以可以看到在q的世界一樣是尤拉定理讓ed消掉。
接著我們來談RSA的 Reblocking 問題:當A要簽暑並加密文件再傳給B,那麼A必須先用自己的private key做簽署,之後再用B的public key加密。但如果B所選的模數比A小的時後,此時便會發生Reblocking,下面例子是擷取自Handbook of Applied Cryptography:

可以看到最後解回m時與原本的不同。要解決此問題可以先看模數大小,模數較小的一方先做,這樣就不會造成reblocking,但基於安全性的考量,如果先進行加密在進行簽署,簽署就不會被加密所保護,攻擊者可能會從此處下手,因此另一種方式是規定兩種key,以t bit來劃分界線,小於此界線的就拿來做簽章,大於此界線的拿來做加解密。
而RSA的加密方式在加密訊息時,會先將訊息切成故定大小再進行簽署,若此時攻擊者調換了不同的block接收方並不會曉得,因此我們會先將訊息經由hash function得到digest,再對這個digest進行簽署,如此一來接收方接收到訊息時,先將訊息經過hash function得到digest,再比對看看這個digest值與傳送方送來的值是否一樣便能得知傳送過程中是否有被竄改過。
接著我們來看比RSA更早之前秘密組織就已經有的類似RSA的演算法:
n = pq
public key : n, private key : p’, q’
($p' \ \ \times \ \ p \ \ \equiv \ \ 1 \ \ (mod \ \ \phi (n)), \ \ q' \ \ \times \ \ q \ \ \equiv \ \ 1 \ \ (mod \ \ \phi (n))$)
Encryption: $C \ \ = \ \ m^n \ \ mod \ \ n$
Decryption: $m \ \ = \ \ C^{p' q'} \ \ mod \ \ n$
這邊跟RSA非常相像,找了p跟q的乘法反元素來消掉n,而令人驚訝的是,RSA加速的方法(中國餘數定理)是在RSA提出後幾年才被提出來了,而這個人居然連加速的方法也想到了:
n = pq, gcd(p, q-1) = 1, gcd(q, p-1) = 1
public key : n, private key : p’, q’
($p' \ \ \times \ \ p \ \ \equiv \ \ 1 \ \ (mod \ \ q-1), \ \ q' \ \ \times \ \ q \ \ \equiv \ \ 1 \ \ (mod \ \ p-1)$)
Encryption: $C_p \ \ \equiv \ \ (m_{p})^{q} \ \ (mod \ \ p) \ \ , \ \ C_q \ \ \equiv \ \ (m_{q})^{p} \ \ (mod \ \ q)$
Decryption: $m_p \ \ \equiv \ \ (C_{p})^{q'} \ \ (mod \ \ p), \ \ m_q \ \ \equiv \ \ (C_{q})^{p'} \ \ (mod \ \ q)$
最後再利用中國餘數定理merge回m就完成了。